How many bars do you see?
|
||||||
| Blivet
(Devil’s Fork) Blivet appeared on the March 1965 cover of Mad magazine, where it was dubbed the “Three-Pronged Poiuyt” (the last six letters on the top row of many Latin-script typewriter keyboards, right to left), and has appeared numerous times since then. |
|||
Figure
2. Two-Pronged Trident |
When
an observer views a two-dimensional picture on paper, he often interprets
it as a three-dimensional figure.
If the figure was interpreted as a two-dimensional figure then it would be entirely possible and commonplace. It's simply three circles connected by a pattern of lines. If it were viewed in this way, then the mind would not be confused at all. "The fascination here is that the drawings are interpreted as representing objects, but the objects represented could not be constructed because the spatial constraints of the environment have been contravened. These pictures work so well because they obey the pictorial rules in local regions but defy them globally. That is, the connections between regions that are presented in appropriate perspective are manipulated, and this creates the impossibility when an interpretation of the whole figure is attempted." (Wade, Nicholas. (1980). Visual Allusions: Pictures of Perception, pg. 16) |
||
In
other words, the figure uses pictorial rules to create the illusion
of three dimensions, but then breaks some of these rules to make
the object impossible to construct. Which rules are followed and
which are broken determines the strength of impossible figures.
A figure which doesn't follow any of the pictorial rules will look
planar, and thus no object will be generated in the viewer's mind.
Conversely, a figure which follows all of the pictorial rules will
be easily represented in three dimensions in the viewer's mind.
The interrelationships between the two opposite guidelines provides
the illusion of an impossible picture. |
Putting
order in the impossible Abstract
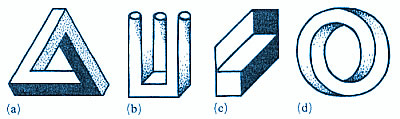
Introduction The presentation of just a few examples of the most well-known impossible figures (figure 3) is sufficient to demonstrate the considerable diversity of types that exists. Many more examples could be given, and it is therefore important to find (or impose upon) these figures some ordering principles and classification schemes.
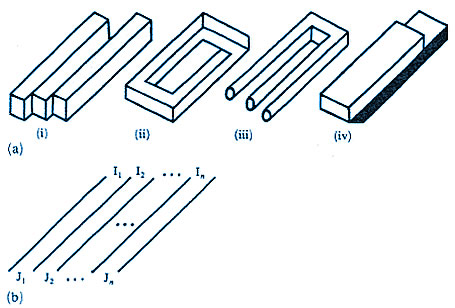
In this paper I propose and briefly discuss several basic ordering schemes. The presentation starts, in section 2, with the definition of an impossible figure (Kulpa 1983) and a general classification that relates impossible figures to possible figures, and also to special classes of figures called 'likely' and 'unlikely' (Huffman 1971; Kulpa 1983). The problem of various degrees of impossibility is also introduced. In section 3 the fundamental 'impossibility sources' are identified (Cowan and Pringle 1978; Kulpa 1983; Thro 1983) as elementary 'building blocks' of all impossible figures. Finally, in sections 4 and 5, two broad classes of impossible figures, namely multibars (Cowan 1977; Draper 1978; Térouanne 1980; Kulpa 1981) and striped figures (Robinson and Wilson 1973), are briefly described. The classification schemes described in this paper are based partially on my own investigations (Kulpa 1981, 1983), and partially on the work of others, especially Huffman (1971) and Cowan (1977). Certain other classification schemes, unrelated, in principle, to those I discuss below, have also been proposed. Guiraud and Lison (1976) tried to systematize, from the graphic designer's point of view, the multitude of ambiguous figures based on the principle behind Thiéry's figure (Thiéry 1895; see figure 3c). On the other hand, Sugihara (1982a, 1982b) suggested the general classification of so-called "labelable figures" (which include many possible and impossible figures) according to features significant for certain types of computer algorithms of automatic scene analysis. Striped
figures
|
|
 |
 |
 |
| |
 |
 |
REFERENCES: |
|
|
| Copyright
© 2004 ABC-people.com Design and conception BeStudio © 2016-2018 |